Line Draw Simulation
Here is a trick/hack to draw a line dynamically on screen.
Demo
Check out this quick demo to see it work.
https://nithindavis.github.io/Axure_demo_lineDraw/linedraw.html
Files
The Axure file for the same is attached here:
lineDraw.rp (57.0 KB)
Concept
The concept behind this trick is school level Math and Trigonometry (quite basic).
If you remember your school days you will recall a very handy theorem called the Pythogaras Theorem, which states that square of the hypotenuse is equivalent to the sum of the squares of the opposite sides.
H^2 = A^2 + B^2
Another theorem in trigonometry tells you that the Tangent(tan) of the angle formed between the hypotenuse and the adjacent side of a right angled triangle is equivalent to the fraction of the length of the opposite side to the adjacent side.
tan(Ø) = a/b
We will be using these two mathematical models to create a line in Axure.
Creating this in Axure
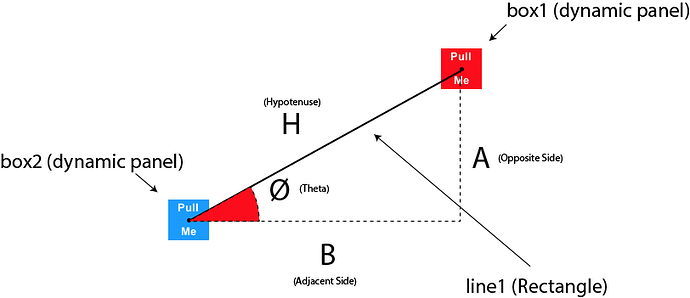
In axure if you want to draw a line between two points, then at any given time the line drawn between two points will form a right angled triangle with an angle theta from the x-axis. The length of this line will be the hypotenuse of the triangle formed.
In order to simulate a line we need two quantities:
- Its angle of rotation (theta)
- Its length
We can calculate these as follows:
Basic Setup:
As shown in the diagram above, we will be using two rectangles (box1 and box2) as our handles and one rectangle(line1) as the line which gets drawn between them.
*If you wish to have the line displayed only when you click and without the handles you can choose to hide them till a mouse click. However for the purpose of this tutorial we will use rectangles visible to keep things simple and understandable.
OnDrag
We will using the OnDrag property of box1 to put all our code.
The first piece of code is to move box1 with drag.
Set the Move function of box1 to move with drag.
Calculate Theta
Declare a global variable called “theta”
Set value of theta using the Set Variable Value function to:
[[Math.atan2(BOX1.y-BOX2.y,BOX1.x-BOX2.x)]]
*BOX1 and BOX2 are local variables set to point to box1 and box2 dynamic panels.
Length of the Line:
Use Set Size function and set the width of line1 to:
[[Math.sqrt(Math.pow((BOX2.y-BOX1.y),2)+Math.pow((BOX2.x-BOX1.x),2))]]
*Again BOX1 and BOX2 are local variables set to point to box1 and box2 dynamic panels.
You may set the height of the line as per your desire. This will become the thickness of the line drawn.
Rotation and PI
Before you rotate the line please bear in mind that the angles returned by the Math functions are always in Radians. However, Axure UI uses Degrees to rotate objects. So we will be converting theta from radians to degrees before we rotate the line.
Using the Rotate function set the angle of line1 as:
[[theta*(180/3.14159265359)]]
*We are basically multiplying theta with 180/PI because 1 PI = 180 degrees.
Moving the line with drag & The Offset Complication
The final step is to move the line accordingly to place it between the two handles.
While this seems to be a fairly simple step it gets a bit complicated due to the way Axure handles its coordinates.
In simple terms Axure maps its coordinates by assuming that the object has not rotated.
Now this brings in a bit of trouble for our line draw experiment. But we can solve this by adding/subtracting this offset values which we will calculate using cosine and sine functions in a way similar to the splitting of force equations into xy components.
Use the Move function to move line1 to the following coordinates:
x:[[BOX2.x-(LINE.width/2-((Math.cos(theta)*LINE.width/2)))+BOX2.width/2]]
y:[[BOX2.y+(Math.sin(theta)*LINE.width/2)+BOX2.height/2]]
*BOX1, BOX2, LINE are local variables pointing to box1, box2, line1 respectively.
Almost Done
Also, put the same sequence of steps into the OnDrag for box2 and you are good to go.
You might wanna use this technique to prototype flow graphs, diagrams and other interactive canvas based activities.
May the force be with you.
Ø